DIDUNAS Eye-tracking Tool
Aim and Background
The DIDUNAS eye-tracking tool allows to identify and characterize student difficulties and under-achievement in mathematics in Grade 1. The eye-tracking tool consists of a series of mathematical activities, the set-up and AI analysis.
The DIDUNAS eye-tracking tool analyzes students’ eye movements when working on mathematical tasks and from this identifies students who are under-achieving and in need of support in mathematics. This way, the eye-tracking tool is a diagnostic tool that can help reserachers to gain fine-grained insights into students’ mathematical activities. It draws on eye tracking as a method that can reveal insights into cognitive processes for appropriate tasks and contexts.
The development of the eye-tracking tool took into account that identifying students’ difficulties at an early age is difficult—not least because young children often lack the ability to report metacognitively on their difficulties. Using eye tracking, the recording of eye movements, for identifying under-achievement in mathematics at the beginning of primary school can circumvent the issue of students’ problems to verbally report on their mathematical difficulties.
The DIDUNAS eye-tracking tool provides a reliable identification method for under-achievement among young students and contributes to an earlier detection, which then allows to support under-achieving students early on.
The DIDUNAS eye-tracking tool has already been used in several studies with over 300 first grade students in two countries (Germany and Cyprus), who could then be supported according to their specific needs.
Mathematical Activities
In the following, examples of the mathematical activities are shown.
Quantities
How many dots do you see?

In order to be able to successfully count quantities of elements, children must know the correct sequence of number words and they must also have other skills. It is essential for the development of counting skills to understand various counting principles (Gelman & Gallistel, 1978), e.g., one‐to‐one correspondence. These counting principles are not innate, but must be learnt (Hasemann, 2007).
Children often master these counting principles before they start school (Briards & Siegler, 1984) and they are often able to count quantities of elements about a year before they start school (Clarke et al., 2008).
Quantity recognition takes place through subitizing, counting, “groupitizing” or pattern recognition (Schindler et al., 2020, 2022).
Quantity comparison
Which is more?

Comparing quantities is an important aspect of early mathematical learning (Beltrán-Navarro et al., 2018).
When comparing quantities, children up to the age of 5 often decide which quantity is larger by counting or on the basis of appearance and extension or overall global impression, even when counting (Piaget & Szeminska, 1952; Schmidt, 1982; Schmidt & Weiser, 1982).
Usually, preschool children do not use counting to compare quantities (Clements & Samara, 2007).
Color pattern
Which color is hidden behind the white blob?

Number pattern
Which number is hidden behind the white blob?
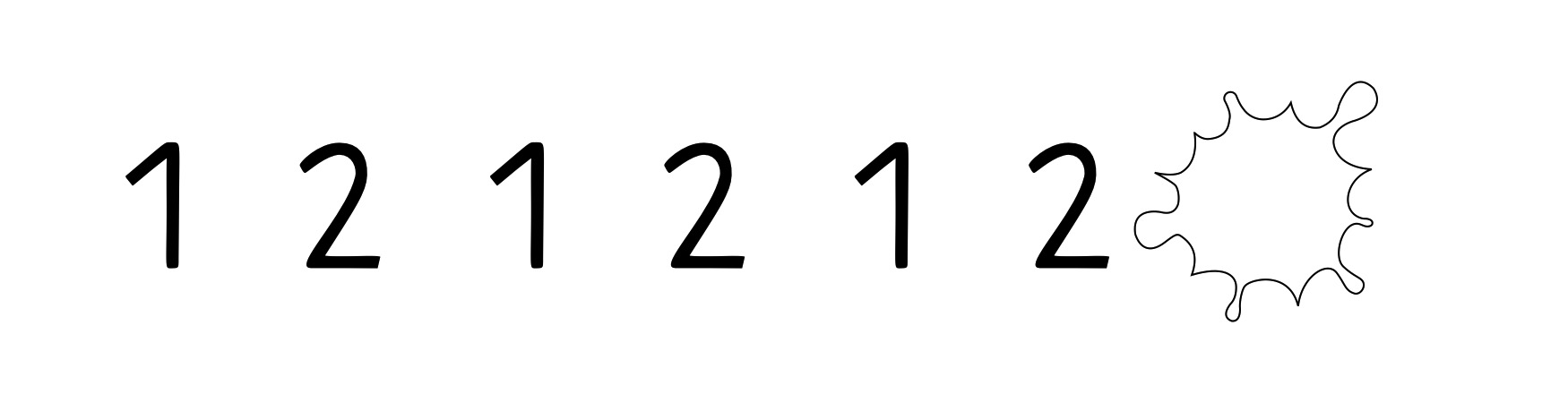
Mathematics can be understood as the science of patterns (Devlin, 2002).
The pattern sequence tasks, both colour patterns and number patterns, are about recognizing regularities, i.e., patterns in ordered sets of elements (Clements & Samara, 2007).
“Patterns and structures” are a central content of mathematics education in primary school (KMK, 2005), with pattern recognition as an important skill in early mathematical learning (NCTM, 2000).
Number line
At which number is the red cross?
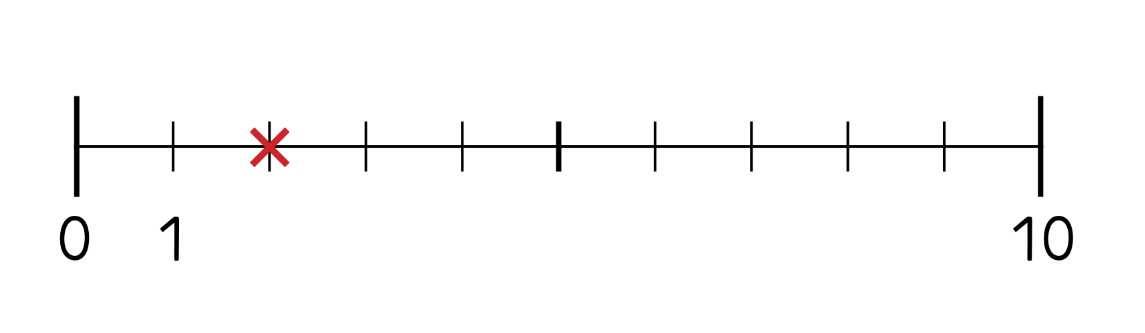
The assignment of a number to a position on the number line appeals to the ordinal understanding of numbers (numbers that are used for ordering).
By the end of kindergarten, children can already use small numbers as ordinal numbers (Clarke et al., 2008). Predecessors and successors of numbers can also be named correctly by many children (Clarke et al., 2008).
Children with difficulties in learning mathematics use structures on the number line less frequently and make more mistakes (Simon & Schindler, 2022; Simon et al., 2022).
Completion to 10
How many dots are missing to 10?
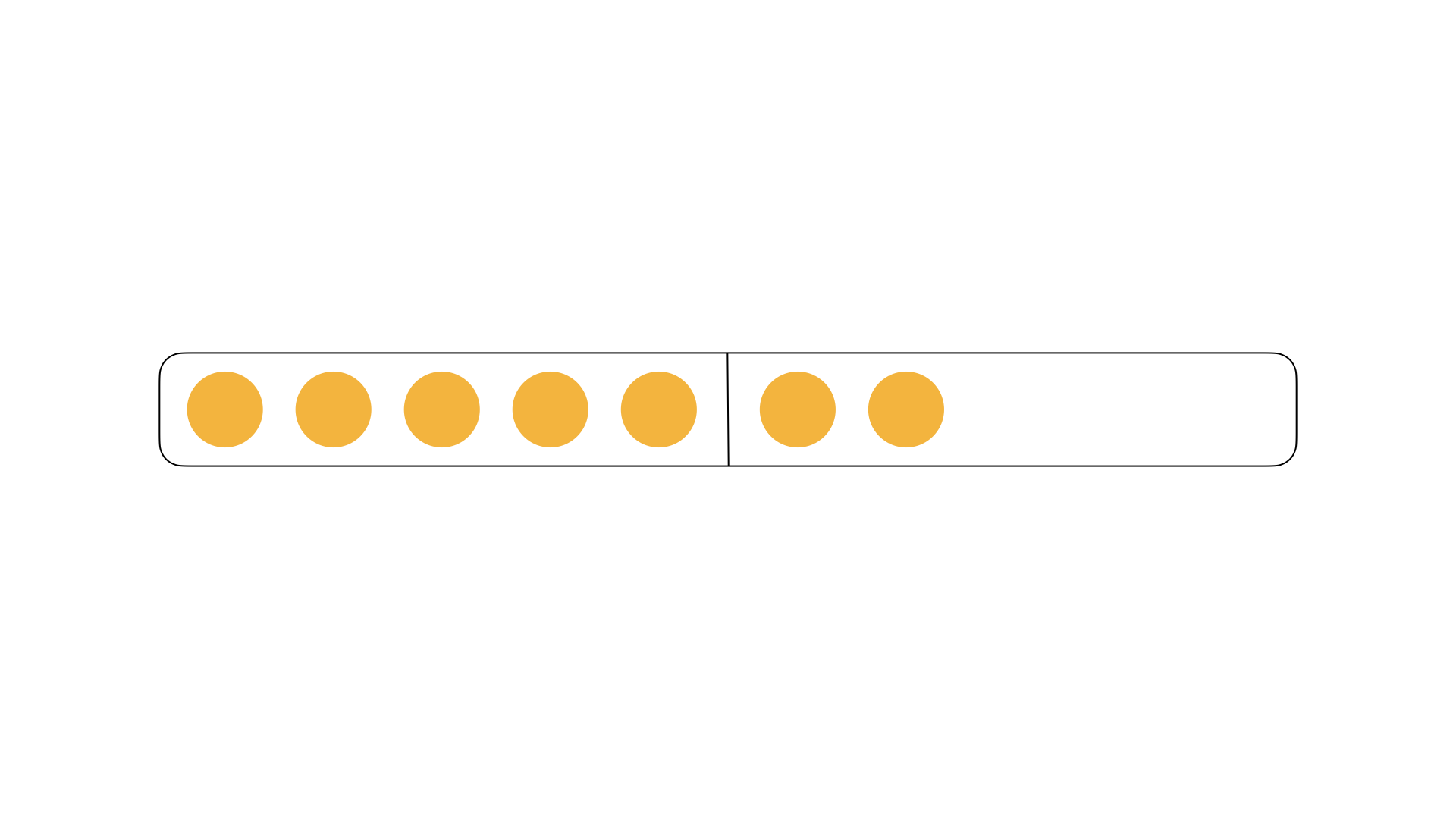
Children at the beginnig of primary school generally have a high level of competence in simple addition tasks (Grassmann & Mirwald, 1995; Selter, 1995; Stern, 1998).
Subtraction tasks, on the other hand, are more difficult for children and they make more mistakes when solving subtraction tasks (Padberg & Benz, 2011).
In general, it is easier for children to perform basic operations when they are given opportunities to act (Padberg, 1996).
Students’ Eye Movements
In the following, examples of students’ eye movements in mathematical actitvities reflecting different strategies are shown. Examples are shown using gaze-overlaid videos and corresponding gaze plots.
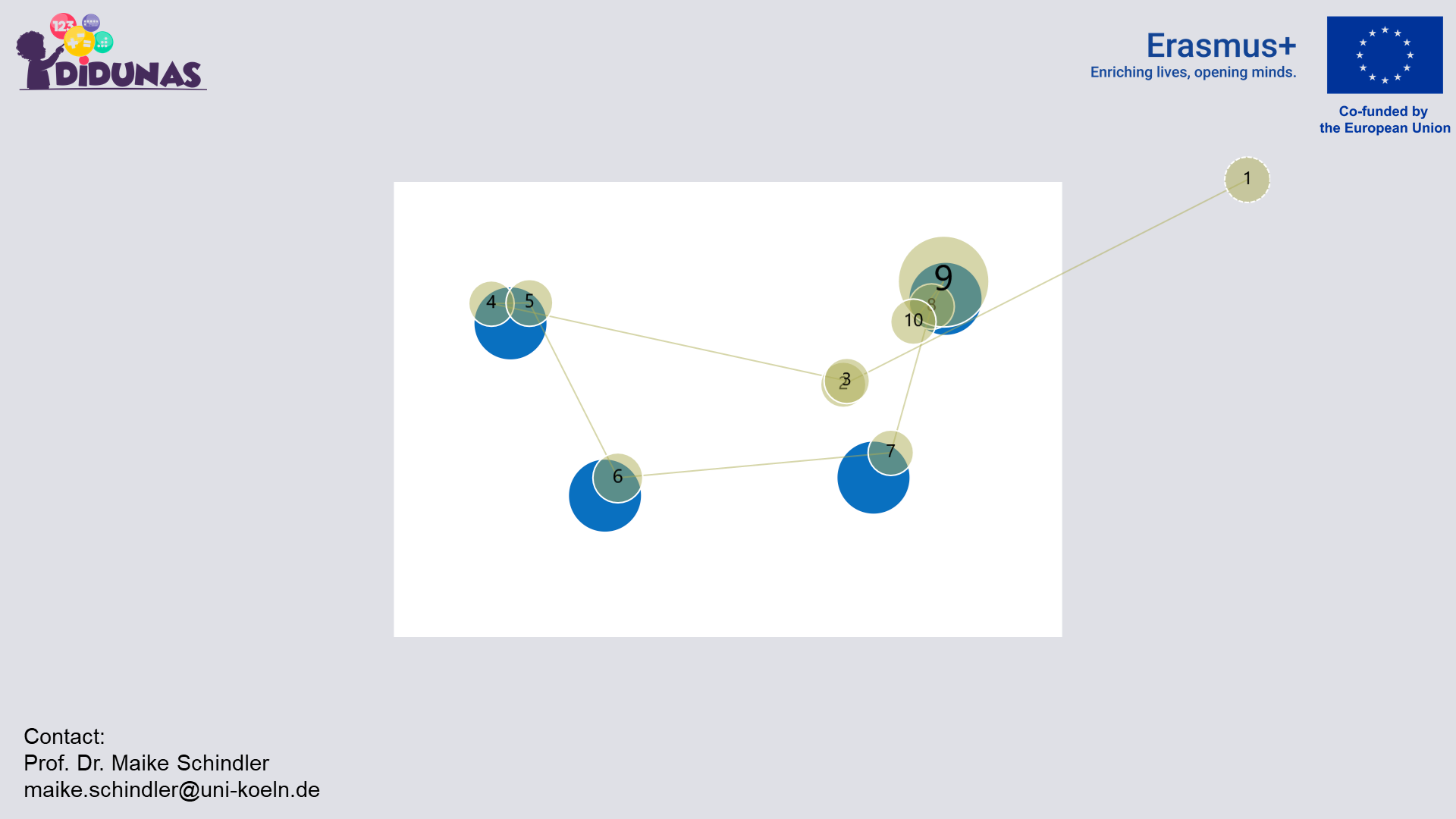
Gaze-overlaid videos are videos in which eye-tracking data is superimposed onto the original visual content. In the gaze-overlaid videos below, students eye movements are visualised as a red wandering dot.
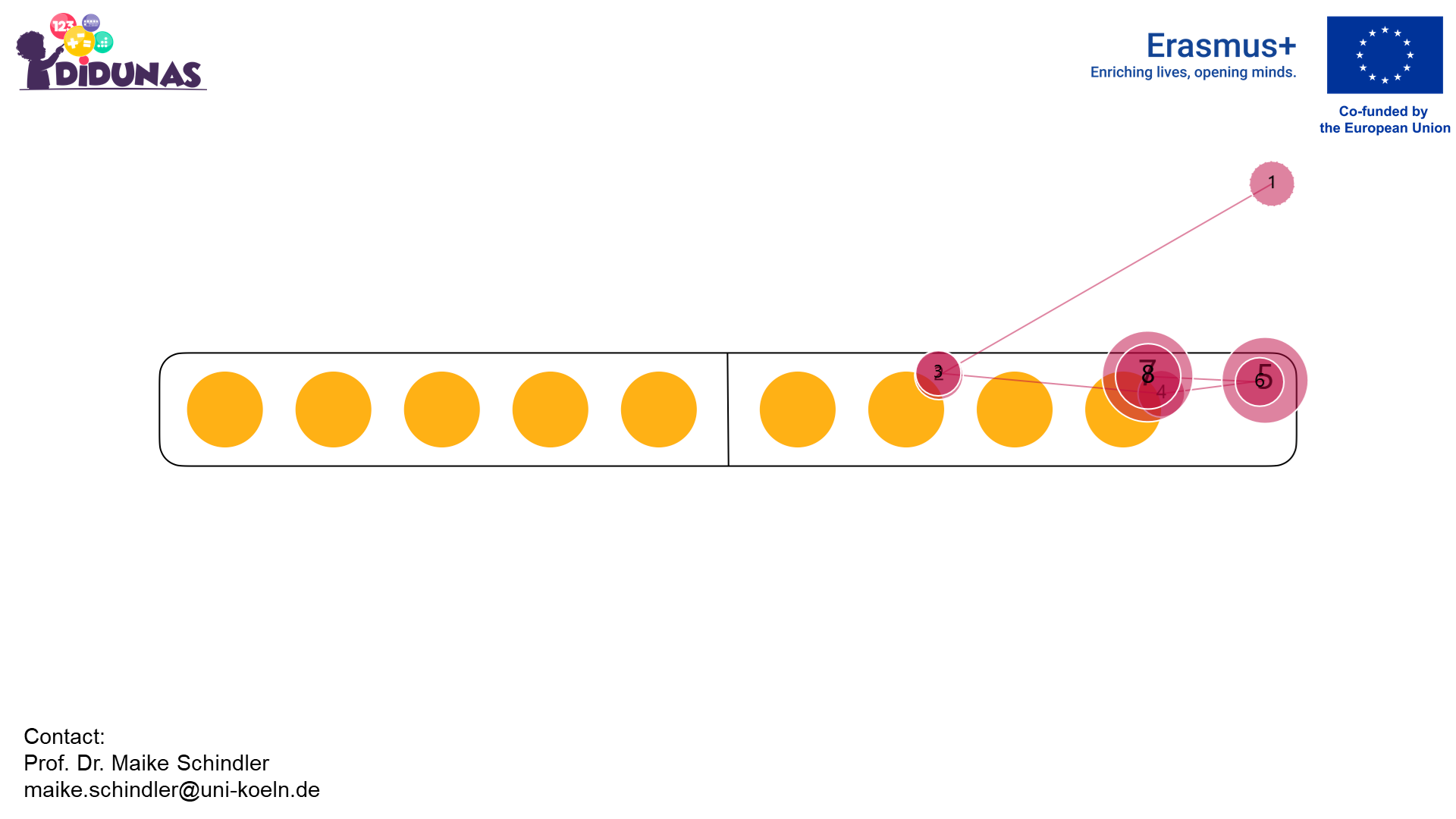
Gaze plots are visual representations that display eye movements over a specific visual stimulus. In the gaze plots, dots represent fixations (periods of relatively stable eye position) and lines connecting these fixations represent saccades (rapid eye movements). The numbers in the dots mark the order of the fixations.
Trough the use of the DIDUNAS eye-tracking tool researchers can analyze students’ strategies when working on mathematical actitvites and gain insights into the reasons for students’ mistakes and how students can be supported accordingly.
Quantities
Quantity recognition through counting
Corresponding gaze plot
Quantity recognition through subitizing
Corresponding gaze plot

.
Quantity comparison
Attending to all dots
Corresponding gaze plot

Simultaneous comparison of the two sets
Corresponding gaze plot
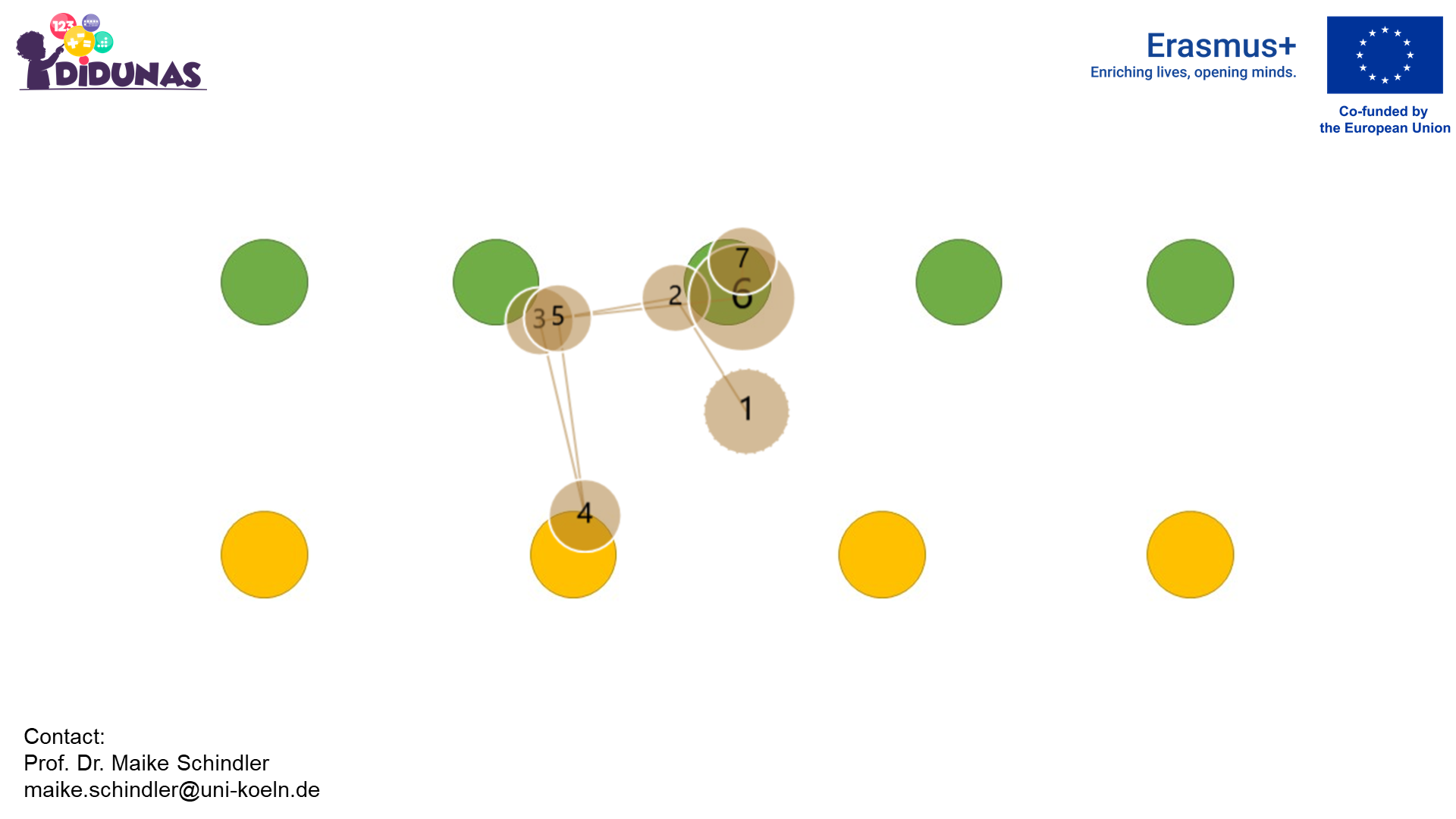
.
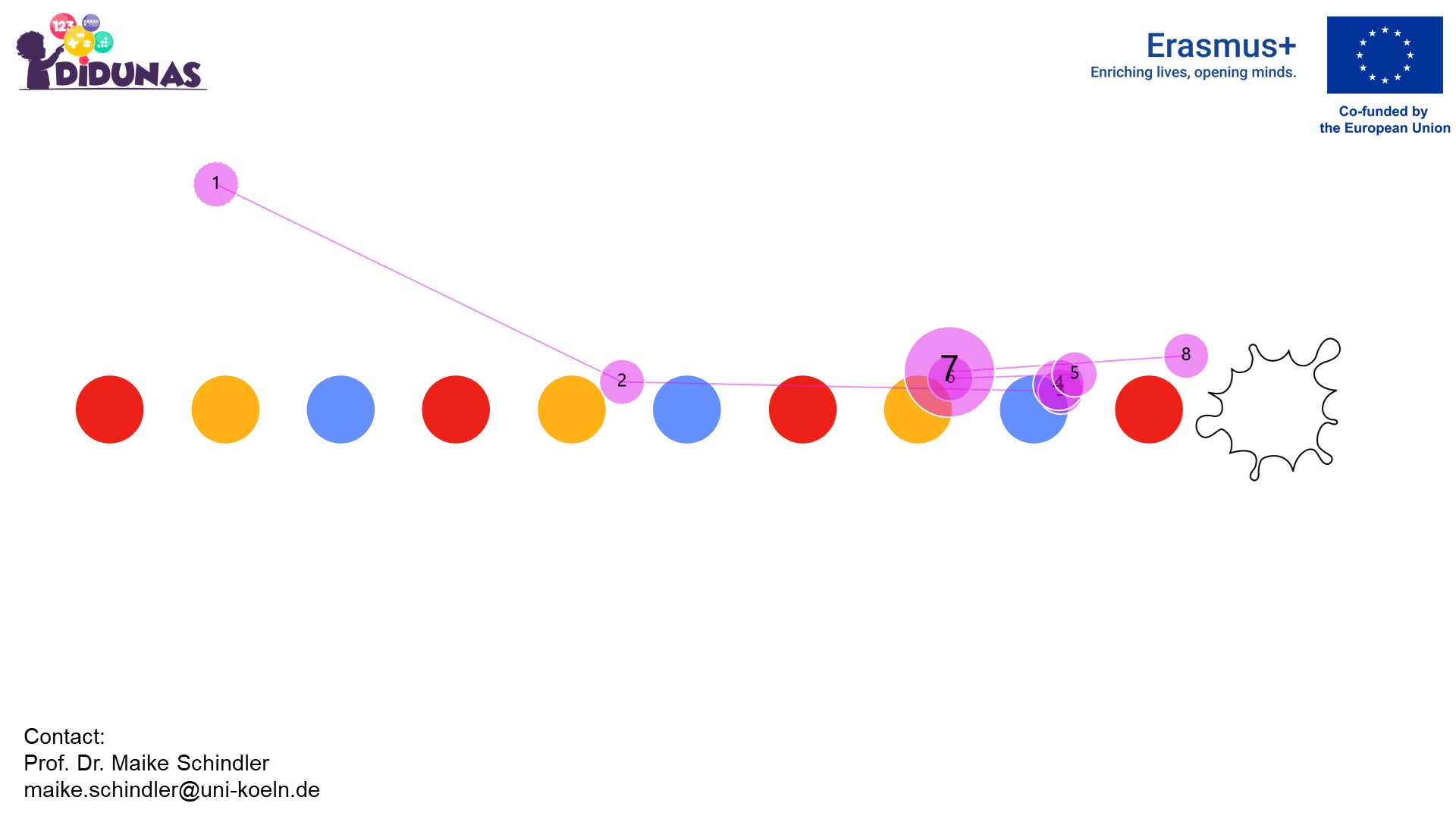
Color pattern
Looking at each element
Corresponding gaze plot
Identifying one unit of repeat
Corresponding gaze plot
.
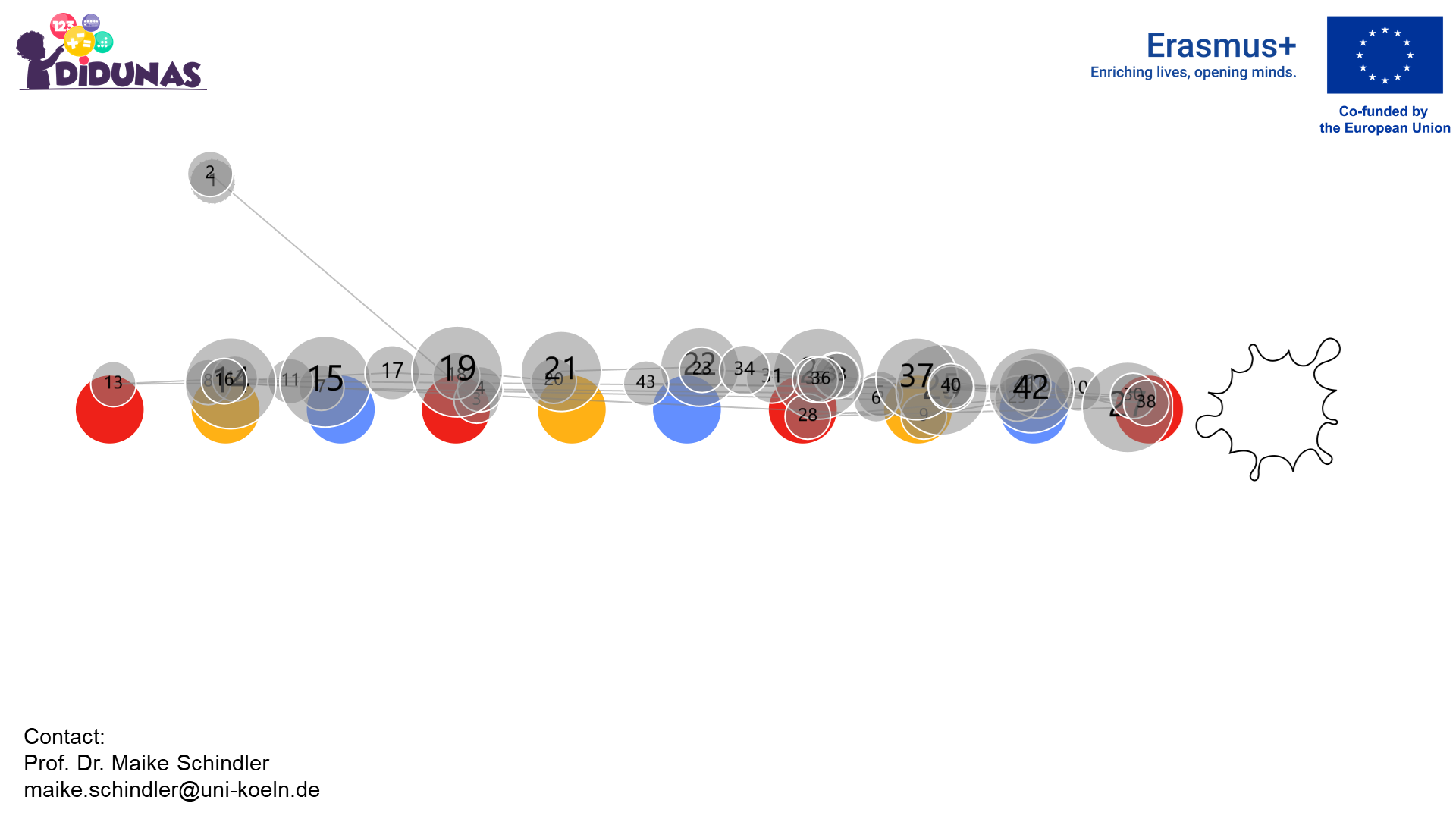
Number pattern
Looking at each element
Corresponding gaze plot

Identifying one unit of repeat
Corresponding gaze plot

.
Number line
Counting from the beginning
Corresponding gaze plot

Direct orientation
Corresponding gaze plot
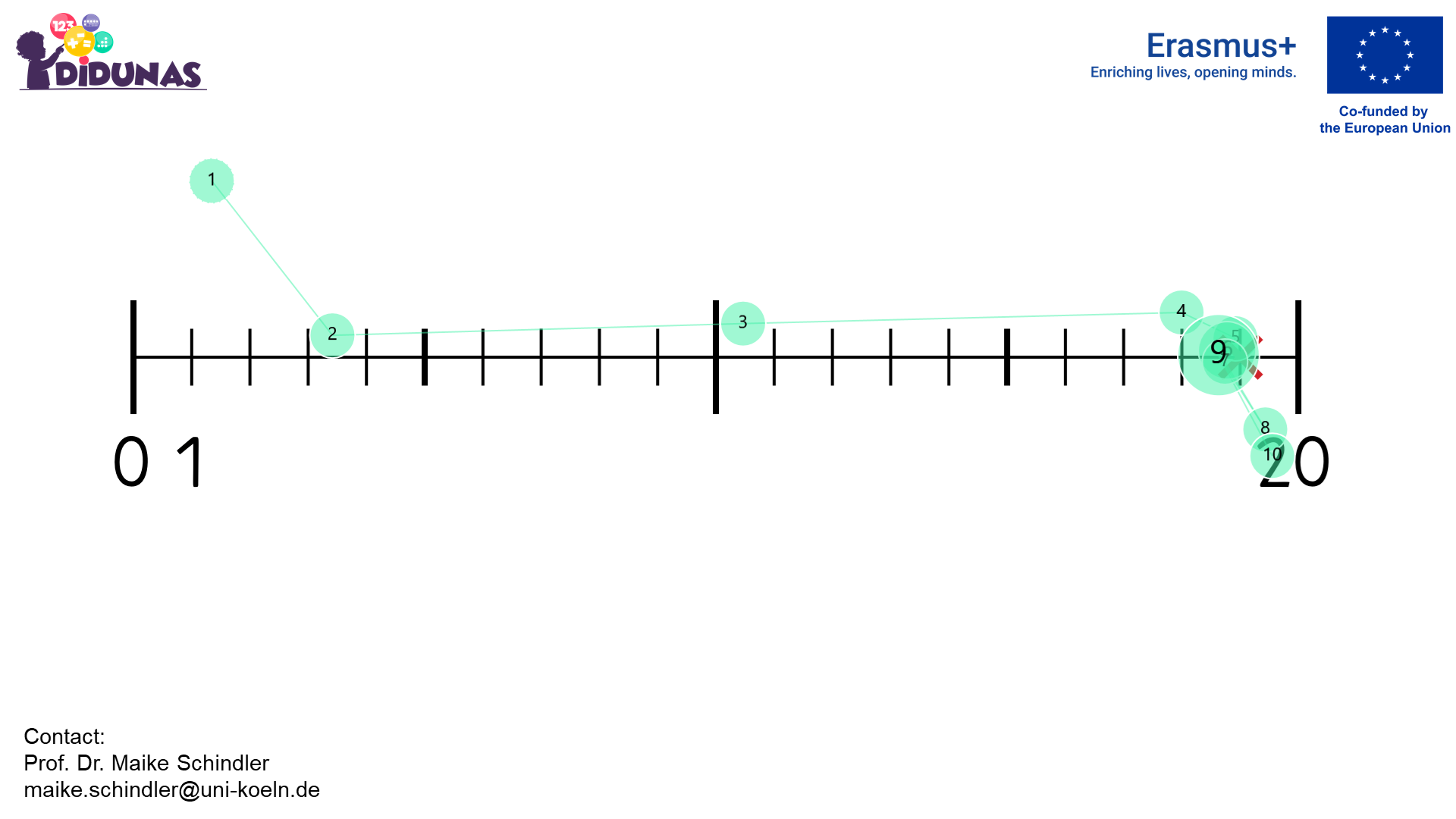
.
Completion to 10
Counting given dots
Corresponding gaze plot
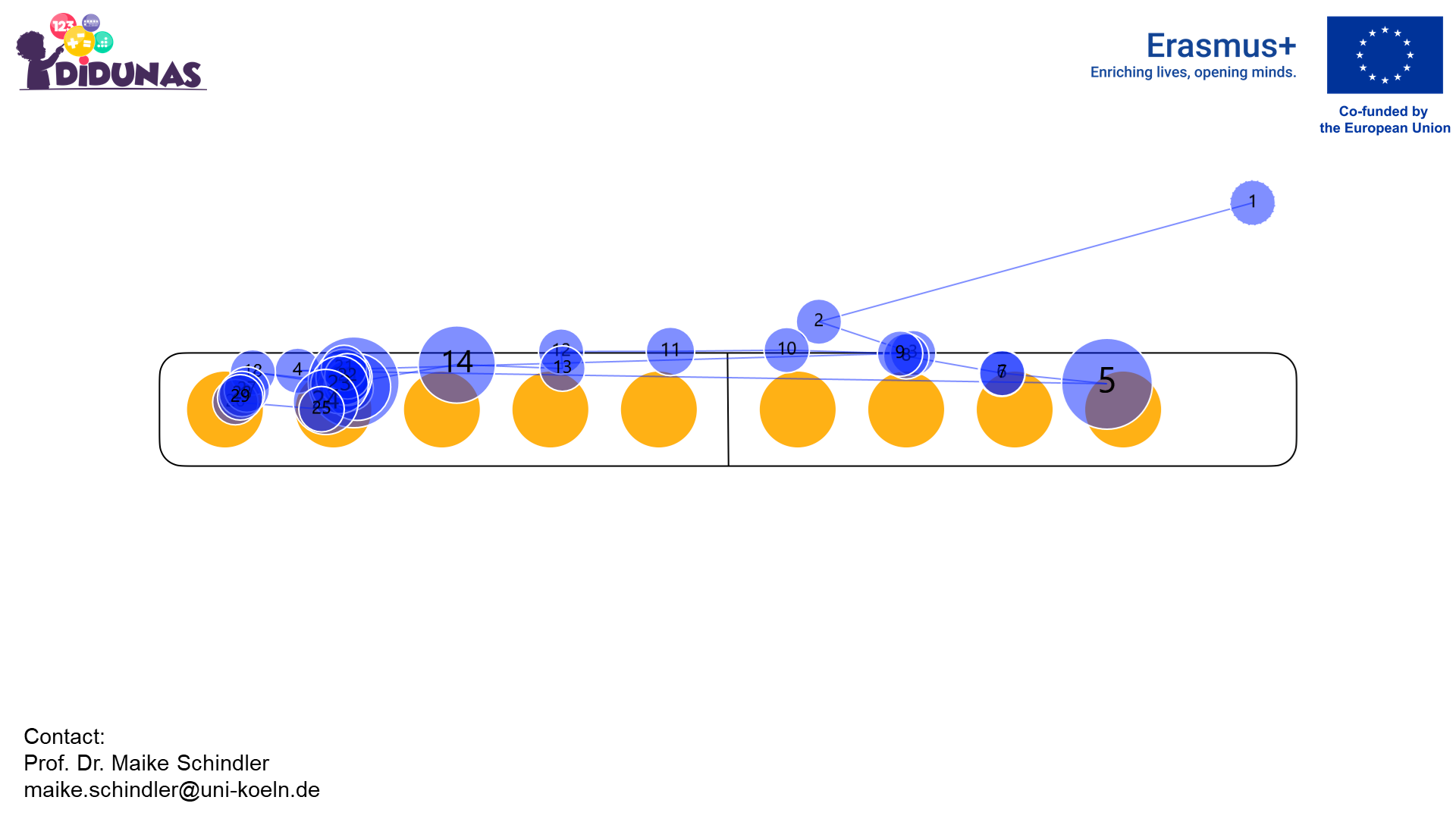
Looking at the missing dot
Corresponding gaze plot
Set-up
In the DIDUNAS eye-tracking tool, the DIDUNAS team used an eye tracker and an eye-tracking software available from Tobii. In Particular, the DIDUNAS ET tool used the eye tracker Tobii Pro X3-120. Tobii Pro X3-120 allows binocular tracking of eye movements using infrared illuminators that generate reflection patterns on students’ eyes. The eye tracker has a sampling rate of 120 Hz. The screen-based eye-tracker Tobii Pro X3-120 is attached to the bottom of the 24-inch full HD monitor (resolution of 1920 x 1080 pixels) where the tasks are displayed. In the DIDUNAS eye-tracking tool, the distance between the students’ head and the monitor is approximately 60-65 cm.
In the DIDUNAS eye-tracking studies, it has been shown that this set-up achieves an average accuracy of eye-tracking data of less than 1°. This corresponds to a maximum error of about 1 cm on the screen. That means that the actual gaze of the students may be at most 1 cm away from that shown by the eye tracker.
The DIDUNAS eye-tracking tool takes these inaccuracies into account: The activities are designed in such a away that meaningful elements are more than 1 cm away from each other.
As eye-tracking software, the DIDUNAS eye-tracking tool uses Tobii Pro Lab which allows to create for example gaze-overlaid videos and students’ gaze plots. The activities are created in a project in Tobii Pro Lab.
Screen-based eye tracker Tobii Pro X3-120


Set up in an DIDUNAS eye-tracking study (Cyprus)
Eye tracker Tobii Pro X3-120 circled in red
Application with school students
The DIDUNAS eye-tracking tool has already been used in various studies with over 300 students to identify under-achieving students in two countries (Germany and Cyprus), who could then be supported according to their specific needs. All of the participating students were first-graders.
Below are two examples of applications of the eye-tracking tool in different primary schools in Germany.


AI Analysis
The AI analyses in the DIDUNAS eye-tracking tool draw on a carefully curated set of mathematical acitivites and tasks that first-grade students work on. The AI-driven approach employs a machine learning predictive model to detect students’ under-achievement in mathematics by understanding the complex, underlying performance patterns on each task. Some of these patterns reveal a risk for the students to develop mathematical difficulties. The AI part of the DIDUNAS eye-tracking tool has been validated using data collected in the DIDUNAS studies conducted in Germany and Cyprus with more than 300 grade 1 students.
Access
The DIDUNAS eye-tracking tool is available and can be used by interested research institutions (conducting research in mathematics education and under-achievement in mathematics in early grades).
Detailed information about the set up, the mathematical activities, and the Tobii Pro Lab project can be provided on request. Support for eye-tracking and AI analyses by the DIDUNAS team can also be requested. If you are interested, please contact Prof. Dr. Maike Schindler: maike.schindler@uni-koeln.de
Please note that an eye tracker (preferably Tobii) and eye-tracking software are required to use the DIDUNAS eye-tracking tool.
